Matlab互換ソフトのOctaveを使ってPID制御のシミュレーションをしてみました。
とはいえ、simulinkもなければ関数もいくつか未実装なので、
伝達関数をちゃんと計算して入力してあげないといけません。
①Octaveのインストール
https://www.gnu.org/software/octave/
からダウンロード,インストールします.
今回はoctave-4.2.1-w64.zipを使用します.適当なフォルダに置いてbinフォルダのoctave.exeを実行すると起動します.
②制御用ライブラリのインストール
pkg install -forge control
少し時間がかかりますが,これでインストール終了です.
ライブラリの使用の際には毎回以下を実行します.
pkg load control
③伝達関数モデルの記述
連続時間の伝達関数
𝑃(𝑠)=1/(1+𝑇𝑠)
を記述するには,以下のように書きます.
%書き方①
T = 13*60;
s = tf(‘s’)
plant = 1/(1+T*s)
%書き方②
plant = tf( [1], [T 1] )
離散時間の伝達関数
𝑃(𝑧)=1/(𝑧−𝑎)
の場合はサンプリング時間Tsを定義して記述します.
Ts = 1 %サンプリング時間[s]
z = tf(‘z’, Ts)
plant = (1) / (z-a)
④PID制御器の伝達関数モデルの記述
連続系のPID制御器の伝達関数は以下になります.
𝑃𝐼𝐷(𝑠)=𝐾_𝑝 (1+1/(𝑇_𝑖*𝑠)+𝑇_𝑑*𝑠)
ただし,連続系の微分要素は高周波のゲインが高くなりノイズが増幅されてしまうため,
1次遅れフィルタを追加した以下の伝達関数が最も用いられます.
𝑃𝐼𝐷(𝑠)=𝐾_𝑝 (1+1/(𝑇_𝑖*𝑠)+(𝑇_𝑑*𝑠)/( 1+0.1𝑇_𝑑*𝑠))
これを③同様に記述すると以下になります.
Kp = 5;
Ti = 750;
Td = 0.1;
P = 1;
I = 1/(Ti*s);
D = ( Td*s ) / ( 1+0.1*Td*s );
PID = Kp * (P + I + D);
⑤閉ループ系の作成
③の制御対象となる伝達関数に④のPID制御器を接続し,フィードバックした伝達関数を作成します.
openloop = ( PID * plant );
closedloop = openloop/(1+openloop);
controlinput = PID/(1+openloop);
⑥ステップ応答とボード線図の確認
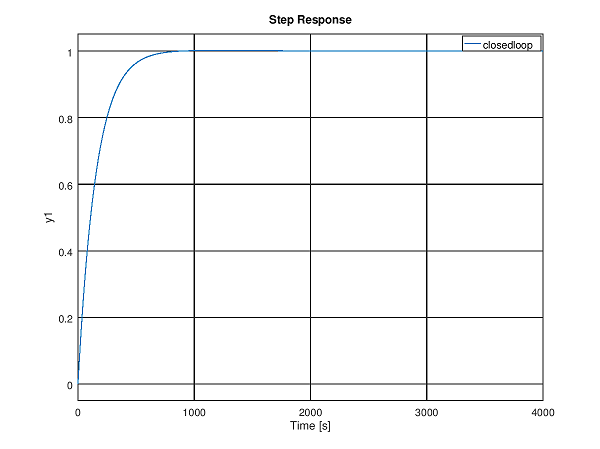
制御対象のステップ応答と制御後のステップ応答をstep()関数で確認します.
それぞれ別の図に表示するよう,グラフウインドウをあらかじめ作っておきます.
PID制御により立ち上がりを高速化できていることがわかります.多少オーバーシュートが出ているので,パラメータはもう少し調整してもいいでしょう.
figure(1);
step(plant);
figure(2);
step(closedloop)
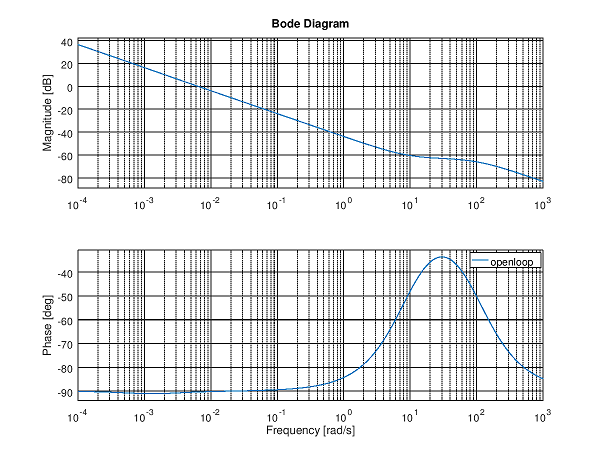
ボード線図はbode()関数で確認します.離散系のボード線図関数dbode()は未実装なので,離散系ではボード線図は容易ではありません...
figure(3);
bode(openloop)
こんな形でPID制御のシミュレーションが簡単にできました.今回のシミュレーションに使ったコードを末尾に記載しておきます.
幾つか関数が未実装であるなど欠点に目をつぶればOctaveでもMatlabに近い感覚でシミュレーションができます.
一方でやはりMatlabのsimulinkの強力さが際立ちます.
個人用途ならMatlabは¥16,500,Simulinkは\4,990なので,このくらいの出費が許容できるかと言ったところでしょうか.